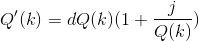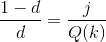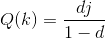Who would win? One Sun sized Earth or 1.3 million Earth sized Suns?

I recently posted a Twitter question asking people to ask crazy science questions, and I'm finally getting around to answering them. Two difference science questions come to mind, but because I'm waiting for Maplesoft to tell me I can have Maple, I am going to pick the easiest question first. The question is of course.

---

Who would win? One Sun sized Earth or 1.3 million Earth sized Suns?

---

The short answer is neither, they both die.

---

Why is the Sun sized Earth Dead?

---

First off the Sun sized Earth is dead, no question. Why? Well first we have to make the assumption that the Earth simply ADDS mass to be as large as the Sun. So how much mass is being added to the Earth? If we assume the Earth is just a sphere we know that the Earth has a radius of 6,371 kilometres with a mass of 5.972 * 10²⁴ kg. The Sun, on the other hand, has a radius of 696,340 kilometres, more than 100x the radius of Earth. Because the mass of an object is proportional to it's volume and the volume of a sphere is proportional the cube of the radius we can calculate that the new mass of the earth is 7.798 * 10³⁰ kg!

That's bloody heavy, on the surface of our new Earth-Sun gravity is 1.073 km/s, this is more than 40x the surface gravity on Jupiter and 4x the surface gravity of our Sun. A house cat would weigh as much as a grand piano on the surface! So that's great, because a lot of pressure and gravitational force means a lot of energy and because our Earth weighs MORE than the Sun you'd expect it would turn into a Sun right?

The problem is the Earth is made of very different things than our Sun. You see the Sun gets its energy from the fusion of hydrogen into helium and this fusion releases a tremendous amount of energy which causes the Sun to expand against the gravitational force the Sun is experiencing. The problem is Earth's core is not made of hydrogen but it's made of iron which cannot be fused to create energy. Iron is the most nuclear stable element in the universe and so changing it into something else such as via fusion (or even fission) actually costs energy instead of gives energy like in the case of hydrogen (or uranium for fission). The outer layers of the Earth have less iron and have elements such as silicon and oxygen that CAN fuse but these requires a tremendous amount of pressure to fuse and even our Earth-Sun is not massive enough to fuse it. The hydrogen found within a planet is simply too sparse to cause any kind of real fusion.

So what would our Earth-Sun become? Well it wouldn't remain a planet, it is simply beyond the size and mass to function as a rocky planet. The tremendous amount of pressure the core would experience would be far beyond what the core would maintain and so the planet would immediately begin to collapse in on itself. The collapse would be equivalent to a stellar supernova as a tremendous amount of energy is released in the violent collapse, dispersing a huge amount of mass outwards. Our Earth-Sun is not QUITE heavy enough to form into more exotic stellar objects like a black hole or neutron star, instead the core collapses to become extremely dense degenerate matter. Degenerate matter is not held up by the electromagnetic force like most matter is, instead it's held up by Quantum Mechanics via a principle called the Pauli Exclusion Principle. In a nutshell matter (specifically fermions like electrons, protons and neutrons) don't like to be in the same quantum state as each other but gravity is trying to force them into the same state by compressing them a tonne and so Pauli Exclusion fights against it in what's called degenerency pressure. The degenernecy pressure is more than the gravitational energy for our Earth-Sun so the core stops from collapsing completely into nuclear matter (IE: Into a neutron star).

Degenerency matter however is extremely dense at about 10000 kg/cm³, this is approximately two million times denser than Earth is. This means our Sun sized Earth quickly becomes much smaller with a radius of just 1776 km according to this website. That's shockingly close to the size of the moon! The surface gravity of the Earth-Sun is now an astounding 165,001 km/s! A house cat on this Earth-Sun would weigh as much as the Titanic! The Earth-Sun is now officially what is called a white dwarf, usually this is the result of a dead star but the Earth-Sun fits the bill quite nicely. The heat of all the energy from gravity and degenerency pressure causes the Earth-Sun to heat up to well above 30,000 C which causes it to shine brilliantly. The Earth-Sun is essentially dead, in that it's not gaining any energy and only losing energy for the rest of it's life, however it's losing energy due to thermal radiation outwards which is fairly inefficient for massive objects so you'd expect the Earth-Sun to shine for a few billion years, maybe much, much longer!

---

Why are the Earth sized Suns Dead?

---

There are two possible answers to this question. The first is a boring one because if we just simply take the components of a star and put them in a mass sized earth we essentially just get a big cloud of gas that behaves pretty inertly. Gravity would heat up the gas and cause the formation of what's called a gas planet (essentially a small gas giant) but there wouldn't be enough energy for fusion and so nothing interesting would happen. Pretty boring. So let's make it more interesting and instead we say what if we got the core of an actively fusing star and then suddenly teleport the core to only have the mass of the earth while the fusion was still ongoing? And what if we repeated that 1.3 million times? 

As said before the Sun produces a certain amount of energy from fusion which fights against the energy due to gravity. The sun fuses 620 million tonnes of hydrogen every second, fusion carries away 0.7% of the mass of mass into energy (the rest forming into helium). Using Einstein's famous E = mc² equation we get that the Sun produces 5.58*10²⁵ Joules of energy per second. That's the equivalent of one hundred million of the most powerful thermonuclear bombs going off at once, every second. 

But unfortunately we have to keep in mind the premise of the question, we're REDUCING the size of the Sun to the size of the Earth so we're gonna reduce the Sun's mass. Using the same proportion as we calculated before we know that the Sun is about 331,000 times heavier than the Earth so we're gonna reduce the energy to that proportion. So for one Sun-Earth we release about 1.683*10²⁰ joules of energy with the fusion stopping immediately because the Sun-Earth is not massive enough to keep fusion going. This is now only 100 times more powerful than the most powerful thermonuclear bomb so it's not nearly as impressive despite the fact we're causing a tremendous amount of destruction. All in all sadly the fate of our Sun-Earth even in this scenario doesn't change much. Essentially a large chunk of gas would be blown away by the explosion but ultimately the explosion probably wouldn't be powerful enough to blow away all the gas and so the gas will eventually condense again after millions of years and form a slightly smaller gas planet. All in all it's a little lame, but we need to remember we have 1.3 million of these little bombs...

---

So who would win?

---

Well as I said before they both kinda die, but maybe the question of who would win is less about who survives and more about how spectacularly they die. So a better question is who produces the most energy? 

We'll start with our Earth sized Suns, we calculated before that one Earth sized Sun produces 1.683*10²⁰ Joules of Energy upon it's death but we have 1.3 million of them giving a total of a massive  2.188 * 10²⁶ joules of energy or over ONE BILLION of the most powerful thermonuclear weapons humanity has ever created all going off at once. That's a very big bomb!

But this, unfortunately, absolutely pales in comparison to the bomb we created with our Sun sized Earth. As I said before the collapse of our Sun sized Earth releases as much energy as a small supernova. To calculate the energy released we notice that the energy comes from the difference in the gravitational binding energy. The equation for gravitational binding energy is given as:

We have to calculate how much energy was released by comparing the gravitational binding energy from when the Earth-Sun was the size of the Sun to when it was the size of a white dwarf (the moon). The initial gravitational binding energy is -1.748 *10⁴³ Joules, that's a LOT but we have deduct it from the gravitational binding energy of our white dwarf which is even more massive at -6.855 * 10⁴⁵ Joules! This means the total amount energy we outputted is a massive 6.837 * 10⁴⁵ Joules! That's 30 quintillion times more powerful than our 1.3 million Earth sized Suns could ever hope to achieve. How many of the most powerful thermonuclear bombs is it? It's 1,000,000,000,000,000,000,000,000,000 many thermonuclear bombs going off.

So both stars die, but the Sun sized Earth dies much more spectacularly than the 1.3 million Earth sized Suns, and now we know!

Is it possible to win this game?

s it possible to win this game?

---

The game

---

You have two players, a Guesser and a Tester. The Tester draws two random cards in a deck of standard playing cards (not including jokers) and looks at the cards without showing the Guesser. In order for the Guesser to win the game the Guesser must deduce with 100% certainty the suit of any one of the Testers cards. The Guesser can ask any yes or no question they like and the Tester answers each question the following way:

1. Look at the first card, ignoring the second card, and ask the question with just the first card in mind. 
2. Now look at the second card, ignoring the first card, and again ask the question but this time only keeping the second card in mind.
3. Decide which answer (1 or 2) you wish to say to the Guesser such that the Guesser gets as little information as possible.

An example, suppose the Tester picked up a hearts and a clubs, if the Guesser asks "Do you have a hearts card?" The guesser would do the following:

1. Look at just the hearts card and ask "Do I have a hearts card?". Answer is yes.
2. Look at just the clubs card and ask "Do I have a hearts card?". Answer is no.
3. Decide to say No (2) to give the Guesser as little information as possible.

The question is can the Guesser always win no matter what the Tester answers?

---

Answer

---

Let's find out. For the proof we'll call the suits of the cards H (hearts), C (clubs), S (spades) and D (diamonds).

Getting rid of the trivial case

First thing we notice immediately is that if the Tester picks up two cards of the same suit then the question is trivially resolved because the Guesser will be forced to answer "Yes" if the Guesser asks if they have a card of that suit. For example if the Tester picked up two hearts and the Guesser asked "Do you have two Hearts?" the Tester looks at both cards individually and both times he is forced to say yes. So for the remainder of this proof we're going to assume the Tester picks up two cards of different suit.

What questions should we be asking

The second part of this is to ask ourselves what questions we should really be asking and what questions the Tester can take advantage of. The first thing we get from the example is that asking for any one particular suit will give no information because the Tester will always be able to say no. One might be tempted to ask a question like "Do you have a hearts AND a spades?" but this question is does not make sense to the Tester and he'll always have to say no. He might look at his Hearts card and ask "Is this both a hearts and a spades?" and the answer is clearly no, it is just a hearts card, so asking whether the tester has both a hearts and a spades card will yield no results. The answer that gives information is not to ask whether the Tester has a hearts and a spades but to ask whether the Tester has a hearts OR a spades, if he has both he'll be forced to answer yes to this question. It only works with two suits though because if you asked whether he had one of three suits (Hearts, clubs and diamonds) he will always have one card in the list and so will always be able to say yes, giving no information.

So now we have some questions to answer, we can go through all six possible combinations of two suits and ask whether the Tester has one OR the other. The Tester will be forced to say Yes to the question that contains both his suits and No to the question that contains neither of his suits, but what about all the other 4 questions? For those 4 he can say whatever he wants. Lets draw up a truth table to describe the possible answers a Tester can give, in this case we will assume the Tester has a H (hearts) and a S (spades)

The truth table is really large because there's 24 different options the Tester can choose from so to narrow it down we'll cut out three obvious cases. The first two cases are obvious.

The Tester says No to every combination except the one he's forced to say Yes to:

In this case it's trivial, we simply pick any one of the two suits for the question he said yes to, he's given away the answer!

The Tester says Yes to every combination except the one he's forced to say No to:

It's simply the negation of our first example, pick any suit outside of the two suits in the combination he said no to. He's given away the answer but in a more roundabout way.

The Tester has said Yes to two combinations but has said No to every other combination:

This one may seem more difficult but it's also trivially solvable. The two combinations that he said Yes to will have to have a common suit and so whatever that common suit is, is the suit that they have. So for example if they said yes to H / C and H / S then it's clear that H is a suit that they have!

Ok so now that we've gotten the easy scenarios out of the way lets talk about the harder scenarios

The Tester has said No to two combinations but has said Yes to every other combination:

This time we can safely determine a suit that the Tester definitely does not have but we can't determine which of the three remaining suits the Tester does have. Let's draw a truth table of possible outcomes to illustrate this point:

Iteration	H / S	H / C	H / D	S / C	S / D	C / D
1	Yes	Yes	Yes	Yes	No	No
2	Yes	Yes	Yes	No	Yes	No
3	Yes	Yes	No	Yes	Yes	No
4	Yes	No	Yes	Yes	Yes	No

In iteration 1 and 3 we can see that Diamonds is the shared suit in the No's so we can definitely say they don't have a diamonds. In iteration 2 and 4 we can see that clubs is the shared suit so we know they definitely don't have a clubs. What we can now is fairly easy, look for a suit combination that is a Yes but contains our excluded suit. For example in iteration 1 we've discarded Diamonds, which means that when he said Yes to the Hearts or Diamonds question, we know that he MUST have a hearts because he CAN'T have a diamonds. For iteration 2 we see he doesn't have a clubs but we also see he said yes to whether he had a clubs OR a hearts so again, we know he has a hearts! It requires a little bit more work but it's fairly obvious when we think about it. Finally we have our final possibility.

The Tester says Yes to half the combinations and No to the other half

This is when the Guesser runs into problems

Iteration	H / S	H / C	H / D	S / C	S / D	C / D
1	Yes	Yes	Yes	No	No	No
2	Yes	Yes	No	Yes	No	No
3	Yes	No	Yes	Yes	No	No
4	Yes	Yes	No	No	Yes	No
5	Yes	No	Yes	No	Yes	No
6	Yes	No	No	Yes	Yes	No

The first thing to notice is that iteration 1 and 6 are trivial, in this case there is a common suit between all the Yes's which means we can safely pick that suit (in 1's case it is Hearts, in 6's case it is Spades). The second thing to notice is 3 and 4 are also solvable because the Yes's both share the common suits and have inconsistencies. For example in 3's case there are two yes cases that contain hearts, 2 yes cases that contain Spades and 1 yes case containing a clubs and 1 yes case containing a diamonds. We can safely say that clubs are diamonds are not the suits the Tester has, so we can easily solve this problem.

The trouble occurs in iteration 2 and iteration 5, the issue is there is no way to distinguish between each iteration. In this case all we are able to do is exclude a suit, in the case of iteration 2 we can safely confirms diamonds is definitely NOT a suit and in iteration 5 we can safely confirm clubs is NOT a suit. But in this case we have three suit contenders and there's no information about which suit is the correct one.

For iteration 2 for example we know that the Tester has a hearts, spades OR a clubs, we know that out of these three the Tester has two of them that's all we can confirm. He's only given us all Yes's for any combination containing any of these 3 suits. We've effectively moved the problem into a three suit problem and this three suit problem is unsolvable, because if you guess any two of three suits you'll always get a yes, so you can just say yes all the time.

Currently I don't believe there's a way to minimize this problem which means the final answer is:

Yes the Tester can always (granted he picks up two different suits) make it impossible for the Guesser to get it right

Informal Proof Printing Money Bridges Gap Between Rich and Poor.

Informal Proof Printing Money Bridges Gap Between Rich and Poor.

One of the big questions about universal basic income (UBI) is "how are you going to pay for it?". While there are many good schemes such as increased taxes that can pay for it, there's one thing a lot of people don't consider. Why don't we just print more money?

Because of inflation right? If we printed more money than the value of money goes down and so no extra value has entered the economy, right? Yes, but I'm here to prove to you that even though no value has actually entered into the economy the poor still get richer at the expense of the rich getting poorer. How does this make sense? Lets find out.

To set up our society suppose we have an economy with some amount of total money M and some amount of total people n. We say we want to print some amount of money C to pay exclusively for universal income. We say that before applying universal basic income the total value of the kth person's worth is given by the function Q(k). Notice I used the word "value" here, value is described simply as the fraction of the total amount of money in the economy that person has, not the total amount of actual money that person has. This will become important when we start talking about inflation because after inflation money is worth less so talking about money in raw terms is not very useful, in UBI everyone gets more money. Instead we want to know how much value that person gets and so we have to make that distinction.

When we're printing new money we cause inflation, the value of a single dollar is worth less than it used to be. I am going to call the degree the value of a single dollar decreases our inflation factor and it's given trivially by this equation.

We also want to know how much money each money (not value) someone will get from UBI, if we assume the money is distributed equally the amount of money someone gets can be given as

This means the total value a person will have after UBI is given out is the total amount of money they have (the money they have initially + the UBI payment) multiplied by the new value of the dollar (the inflation factor). Describing this equation:

Factoring out we get

Great but we care about how their value changes not their absolute new value, we can calculate this by simply dividing their new value by their old value to give us.

So lets notice something here, d and j are both constants so the only variable on the RHS is the initial money we started with. The proportion of gain or loss we get is inversely proportional to the amount of money we initially had. The more money we had the more loss we should expect, the less money we have the less loss we should expect. This means that poor people should expect greater benefits from UBI than rich people even when factoring into account inflation, but how good are these benefits really?

To figure this out we should ask ourselves how much money do we need to break even, ie: not gain or lose any value after UBI. If we have more than this amount of money we should expect to lose value and if we have less than this amount of money we should expect to gain value. We can figure this out by setting the LHS side to 1 and solving.

Great! But this form of the equation is a little abstract, let us expand out the inflation factor d and the UBI income per capita j to see something quite interesting...

That's right in order to break even the amount of money you need to start with is the average amount of money in the society. If you have below average income you will GAIN value and if you have above the average you will LOSE value. Therefore printing money favours the poor at the expense of the rich! Woohoo we've solved it right?

"But surely the rich could raise prices, and then make UBI useless!"

Argh those dastardly rich! But are we actually sure that the rich raising prices will disadvantage the poor? Let us investigate, to model this we should introduce a price of a good, we'll call the value of the good G so that the number of goods (A for amount) someone can buy is simply given as

Notice that G here is once again value not money. If we were to call the value of the good after UBI is implemented (and the rich raise prices) G' then the equation:

Does NOT mean the prices of the good hasn't changed, it means the VALUE of the good hasn't changed or that the price of the good increased with inflation exactly. Noting that we will introduce a factor q which is an arbitrary factor that is how much the rich increased the items value after UBI. Giving the new value of our good as:

If q is greater than one then the rich have raised prices unfairly and if q is less than one then the rich have failed to raise prices and the poor are unfairly advantaged. If q is exactly equal to one than the rich have done the right thing and have raised the prices of the good exactly proportional to the amount of inflation. The new number of items a person can buy is now equal to their new value divided by the new value of the good.

Expanding out Q'(k) gives us our final equation

We want to know whether someone can buy MORE goods or LESS goods so we divide the new amount of items someone can buy with the previous amount of items someone can buy

Doing some cancelling we get

Cool! So now we know how much more a specific person can buy but once again we want to know who is advantaged (can buy more) and who is disadvantaged (can buy less). To figure this out we once again set our LHS to 1 to find out what value you need to break even, if you are above that value you will be able to buy less and if you are below that value you will be able to buy more. Solving we get:

Great! Somethings to note here. Lets suppose prices do not change with inflation, what happens here? In this case q is exactly equal to the inflation factor d which means we get a division by 0, that seems broken but it's not it just means there is no solution to this equation which means no matter how much money you have you'll ALWAYS be able to buy more goods. This makes sense because again, everyone gets more money so if the prices don't change to reflect that then everyone's buying power increases.

Ok but what happens if the rich do the right thing and increase their prices with inflation, in this case q just becomes 1 and we get this familiar equation again:

Low and behold that's the exact same equation we got before and once again when we expand d and j we get.

That's right even if prices increase with the resulting inflation the poor still can buy more if they have less than the average income. Why? Because even if the rich get the same value for the goods that they're selling the value still initially changed to favour the poor when UBI was introduced so the poor STILL have more buying power even when you take into account a price increase.

What if the rich raised the prices even more, beyond inflation? First of all, yes this certainly COULD happen but the rich don't need UBI to do this, they can increase prices unfairly right now! The mechanisms that are stopping the rich from raising the prices of goods arbitrarily high right now will still exist even after UBI is implemented. But suppose the rich did raise prices higher than inflation, what would happen? 

Well you can plug in some random values of q, any value greater than 1 unfairly favours the rich and any value less than 1 unfairly favours the poor. But for values greater than 1 you'll notice something, there will always be an amount of money that you can have, below which, you will be able to buy more items. When q is greater than 1 the rich do get richer and the middle class gets poorer but the lowest class STILL manages to get richer, this stops becoming true when q is so high that the amount of money you need to have less of is smaller than the price of a single good. Can the rich raise prices so drastically high? Of course, but again whether they could do that isn't a question of UBI, they could raise prices this high with or without UBI and it'd have the same effect, people can buy less items.

Anyway I hope that clears up why printing money to pay for UBI can still have a beneficial effect on society.

Scientism and the failures of Democracy.

  I've been thinking of the best society, a society that will benefit humanity for generations to come. I believe the currently proposed forms of society have issues that we see a lot and are not easily buffered out. For example:

  - Capitalism is great for explosive expansion and technological advancement but it does this indirectly. It promises those who can advance products chosen by the masses a reward in the form of capital, but this indirection is what leads to loop-holes and corruption by simply advancing capital through any means necessary (such as forcefully). It also creates what's akin to a weighted democracy, where every dollar becomes a vote and those with the most dollars are able to reform the society to make sure they stay above the rest, leading a very large vector for corruption.
  - Communism creates equality through shared distribution and a value of community but in order to create such a society a vast amount of power is required to be placed in a relatively small set of hands. Crafting a communist society with the correct logistics and organisation requires a large centralisation of power which creates a large vector for corruption that can be attacked, many communist countries become totalitarian for this very reason.
  - Democracy is great at fighting off corruption by giving everyone a chance to vote but intelligence and ability is represented as a bell curve and democracy necessarily limits humanities potential by placing the power in the average person and not the exceptional person. With the very manipulative psychology of humanity as well, we can create vectors of corruption through charisma as opposed to logic.

All of these systems have something in common that causes them to fail and be sub-par, corruption and the limitations of human bias and psychology itself. The greatest system is one that is driven by objective data, measured by many sources and free of corruption and led by the people who can most drive and interpret this data. A technocratic society. Here's how we could do that.

The Corruption Problem:

Any society that requires some kind of oligarchy rule will have a significant vector of corruption that must be addressed in order for a society to succeed. Corruption in itself is difficult to define, but in this article I define it as the means in which a small group of people can knowingly impact a large group of peoples lives against their ultimate interests for self-serving reasons. A dictator is corrupt if he works for his own self interest at the expense of the people around him, but a dictator is not corrupt if he works entirely for the benefit of those people around him. Importantly corruption is different to incompetence, where someone with good intentions may actively harm a larger group of people. Our theory here is the technocratic aspect of this society (talked about later) will mitigate the impact or risk of incompetence. No here we must talk about corruption and how to avoid small amount of people even with the greatest echelons of power changing, damaging and warping society to their self interests.

The answer lies in an anti-corruption body, I call the corruptum. The corruptum has ultimate power in the society, can imprison people of other departments no matter their level of power and can request documents even of the highest secrecy and intelligence. But creating such an organisation doesn't cure the corruption problem, it simply moves it to the corruptum itself, if we have a body to weed out corruption that has ultimate power what's to stop this organisation itself being corrupt? The problem is at least easier solved in the corruptum because we can design a department who attempts not to be efficient but instead to be correct and secure in fighting corruption.

Corruption is mitigated through multiple ways, increasing the number of people required to accept the corruption, distribution of power to avoid centralisation and most importantly of all, a level of conflict. Conflict is the ultimate battle against corruption, corruption relies on the innate behaviour for humans to be self-serving and not cooperative but this is also the essence of conflict, to have two individuals with different self-serving ideals. Thus creating a department that doesn't shy away from conflict but instead thrives on conflict, this is important in creating our corruption-free corruptum because instead of trying to make people less likely to be self-serving we instead capitalise on the self-serving nature of humans.

The corruptum is split into multiple cells of equal authority, I'd anticipate at least 16 cells with a max around 100. There is no central authority within the corruptum, each cell acts with equal and absolute authority. Each cell is divided into two equal parts, the first part is responsible for seeking out corruption in all the other departments of the society (talked about later), the second part is responsible for seeking out corruption in other cells of the corruptum. There is no zoning or restriction, each cell is capable of investigating any other cell or department regardless of region. Any action the corruptum seeks to do that would require the arrest of a person or confiscation of documents must be approved by two other corruptum cells (randomly chosen and different every time). The number will be increased for the highest levels of authority to 6 randomly chosen cells (and the agreement must be unanimous). Any corruptum cell that discovers corruption will be financially rewarded, any corruptum cell that discovers corruption within another corruptum cell will be even more financially rewarded.

Why should this system work? Each cell works independently of all the other cells and is actively rewarded and encouraged to work AGAINST the other cells. Any cell seen violating the rules will immediately be dog-piled by the other cells for their financial reward, any cell that does this unnecessarily or entirely for the financial means will also be dog-piled by other cells. The essence is that this department will have an incredible amount of churn and conflict within itself, something to be avoided generally but here is encouraged to weed out the ability for corruption to manifest itself. What this creates is a department that is incredibly inefficient but necessarily so, the splitting of the cell into two different parts helps to mitigate the inefficiency when dealing with other departments. But the active nature of the corruptum is one of necessary and rewarded hostility towards everyone and everything, where self-serving philosophy is rewarded and people are pitted against each other. Importantly the corruptum does not have the ability to change law, only to arrest individuals for what they see as corruption. In order to maintain a corruption free corruptum we keep the hostility between the corruptum cells using self-serving financial reward. Spreading out the corruptum cells and fostering a culture of hostility between cells should also help protect mass-cell cooperation.

The Assembly:

With the corruptum in place to mitigate corruption within the society we need to now define the other departments and importantly define who actually makes the laws. This is done in the assembly, an amalgamation of different departments across society that all vote on different measures. Each department has an assigned number of votes which are unequal based on department, motions are passed by the number of votes altogether in the assembly unless otherwise specified.

The assembly (and corruptum) is guided by a constitution that cannot be changed unless a referendum is proposed. In order for a referendum to go through there must be a vote where a majority of the Scientia, the Socialite (talked about later) and the Corruptum agree to pass the vote. So what are the departments?

The Scientia:

  The Scientia is the largest department and controls the largest amount of votes in the assembly. They are the technocratic side of our society and represent study, investigation and analysis of scientific results in order to make governed decisions on the society. Central to the scientia's organisation is what is known as The Grand Plan, a wide ranging, transparent, open and cited justification for the laws being pushed by the Scientia. More on this later.

  The Scientia is headed by Scientia representatives, considered by their peers as the most expert in their field. They are the representatives in the assembly and have a limited term limit (example, 6 years). They are the ones that vote in the assembly and debate the different results and recommendations seen in the grand plan. They are closely watched by the corruptum as is all of the Scientia department.

  What drives all of the Scientia's decisions is The Grand Plan, a document or series of documents open to the public that consolidates the accumulative results of scientific studies across many different disciplines and many different organisation. Anyone can submit results to The Grand Plan and Curators (employees of Scientia) decide which studies have a level of rigor to be accepted in The Grand Plan. A single curator is given to a proposed study, this curator then makes a judgement on the study. This judgement is sent to two other (randomly chosen) curators who either agree or disagree on the judgement, if both curators agree the judgement passes, if any curator disagrees the study is given to another curator and the process repeats. When a judgement is passed all three curators must send their results and reasoning to the corruptum, this is then given to a random corruptum cell who may either choose to accept the judgement or ponder for further investigation. If pondered for further investigation it is sent to two other corruptum cells who can either let the investigation pass or can accuse of corruption which follows the normal procedure.

  Importantly The Grand Plan is seen as a massive meta-study as opposed to a truth. This means that The Grand Plan can have two studies submitted to it that contradict each other. This is fine, it is up to the Scientia department to debate the conflicting results and decide, via a democratic process within the Scientia, which result should be taken or whether more data is needed to make a judgement. Even if it is decided that one study holds more weight than another study, the conflicting study must still be within The Grand Plan for transparency sake and in case future studies back up the conflicting studies claim. At the end of it all for every topic an ultimate judgement must be made that gets revised when any new study on that topic is added, the ultimate judgement is a recommendation of law that supports the judgements findings. This might be things such as supporting green infrastructure, or putting more budget in a field of study, or even sociological things.

The Socialite:

  Not all things can have data generated about them, a society should also be happy and healthy and feel there is a level of freedom within the society, this is where the socialite comes in. The Socialite is the democratic arm of the society and acts as the second largest department in the assembly (with strictly less votes than the Scientia). The Socialite acts in a very similar way as our current democratic society with a little less power and a few other changes.

For one the socialite must always have 5 political parties running in any election, no external money is given to any political party and their budget for voting is fixed and decided by the assembly. Political parties are chosen via a general preliminary election in which personal money can be used but the sources must be explicitly stated. The 5 political parties that are chosen must be chosen with a diverse set of political beliefs, this is verified by the Corruptum who must decide if the political parties are diverse enough. Alliances between political parties in the general election is strictly forbidden, but agreements on policy are ok. Beyond this the democratic system within the socialite works similar to a normal commonwealth, with a congress, house of representatives and a prime minister.

Within the assembly as a whole it will be generally accepted that any decision the socialite comes up with that does not conflict with The Grand Plan should be passed. This is enforced by the Scientia voting on recommendations made by The Grand Plan, recommendations made outside of The Grand Plan can't be effectively voted towards by the Scientia so will generally be deferred to the Socialite. If the socialite decides to vote for something within The Grand Plan then it is put up to a wider assembly vote. In general a one-to-one head of the Scientia vs the Socialite should favour the Scientia, but other departments (of much smaller vote than both the Scientia and the Socialite) may weigh in towards the socialites favour. As well each member of the Scientia and Socialite have their own vote so it is possible for a minority of the Scientia to vote against the majority, and will be generally expected to be the same for the Socialite as well. Thus it is possible that a Socialite that agrees on a topic and a Scientia that is conflicted will favour the Socialite. Basically the Scientia should control about 46% of the vote, while the Socialite should control around 42% of the vote with the remaining 12% delegated to various other minor departments.

Minor Departments:

I have not finished finalizing the minor departments, but minor departments so far include the Militarium, which controls the military and acts for military affairs. The Economus which is a representative of free businesses and so forth. In general this is all I have constructed so far.