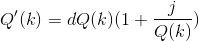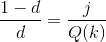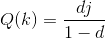Is it possible to win this game?

s it possible to win this game?

---

The game

---

You have two players, a Guesser and a Tester. The Tester draws two random cards in a deck of standard playing cards (not including jokers) and looks at the cards without showing the Guesser. In order for the Guesser to win the game the Guesser must deduce with 100% certainty the suit of any one of the Testers cards. The Guesser can ask any yes or no question they like and the Tester answers each question the following way:

1. Look at the first card, ignoring the second card, and ask the question with just the first card in mind. 
2. Now look at the second card, ignoring the first card, and again ask the question but this time only keeping the second card in mind.
3. Decide which answer (1 or 2) you wish to say to the Guesser such that the Guesser gets as little information as possible.

An example, suppose the Tester picked up a hearts and a clubs, if the Guesser asks "Do you have a hearts card?" The guesser would do the following:

1. Look at just the hearts card and ask "Do I have a hearts card?". Answer is yes.
2. Look at just the clubs card and ask "Do I have a hearts card?". Answer is no.
3. Decide to say No (2) to give the Guesser as little information as possible.

The question is can the Guesser always win no matter what the Tester answers?

---

Answer

---

Let's find out. For the proof we'll call the suits of the cards H (hearts), C (clubs), S (spades) and D (diamonds).

Getting rid of the trivial case

First thing we notice immediately is that if the Tester picks up two cards of the same suit then the question is trivially resolved because the Guesser will be forced to answer "Yes" if the Guesser asks if they have a card of that suit. For example if the Tester picked up two hearts and the Guesser asked "Do you have two Hearts?" the Tester looks at both cards individually and both times he is forced to say yes. So for the remainder of this proof we're going to assume the Tester picks up two cards of different suit.

What questions should we be asking

The second part of this is to ask ourselves what questions we should really be asking and what questions the Tester can take advantage of. The first thing we get from the example is that asking for any one particular suit will give no information because the Tester will always be able to say no. One might be tempted to ask a question like "Do you have a hearts AND a spades?" but this question is does not make sense to the Tester and he'll always have to say no. He might look at his Hearts card and ask "Is this both a hearts and a spades?" and the answer is clearly no, it is just a hearts card, so asking whether the tester has both a hearts and a spades card will yield no results. The answer that gives information is not to ask whether the Tester has a hearts and a spades but to ask whether the Tester has a hearts OR a spades, if he has both he'll be forced to answer yes to this question. It only works with two suits though because if you asked whether he had one of three suits (Hearts, clubs and diamonds) he will always have one card in the list and so will always be able to say yes, giving no information.

So now we have some questions to answer, we can go through all six possible combinations of two suits and ask whether the Tester has one OR the other. The Tester will be forced to say Yes to the question that contains both his suits and No to the question that contains neither of his suits, but what about all the other 4 questions? For those 4 he can say whatever he wants. Lets draw up a truth table to describe the possible answers a Tester can give, in this case we will assume the Tester has a H (hearts) and a S (spades)

The truth table is really large because there's 24 different options the Tester can choose from so to narrow it down we'll cut out three obvious cases. The first two cases are obvious.

The Tester says No to every combination except the one he's forced to say Yes to:

In this case it's trivial, we simply pick any one of the two suits for the question he said yes to, he's given away the answer!

The Tester says Yes to every combination except the one he's forced to say No to:

It's simply the negation of our first example, pick any suit outside of the two suits in the combination he said no to. He's given away the answer but in a more roundabout way.

The Tester has said Yes to two combinations but has said No to every other combination:

This one may seem more difficult but it's also trivially solvable. The two combinations that he said Yes to will have to have a common suit and so whatever that common suit is, is the suit that they have. So for example if they said yes to H / C and H / S then it's clear that H is a suit that they have!

Ok so now that we've gotten the easy scenarios out of the way lets talk about the harder scenarios

The Tester has said No to two combinations but has said Yes to every other combination:

This time we can safely determine a suit that the Tester definitely does not have but we can't determine which of the three remaining suits the Tester does have. Let's draw a truth table of possible outcomes to illustrate this point:

Iteration	H / S	H / C	H / D	S / C	S / D	C / D
1	Yes	Yes	Yes	Yes	No	No
2	Yes	Yes	Yes	No	Yes	No
3	Yes	Yes	No	Yes	Yes	No
4	Yes	No	Yes	Yes	Yes	No

In iteration 1 and 3 we can see that Diamonds is the shared suit in the No's so we can definitely say they don't have a diamonds. In iteration 2 and 4 we can see that clubs is the shared suit so we know they definitely don't have a clubs. What we can now is fairly easy, look for a suit combination that is a Yes but contains our excluded suit. For example in iteration 1 we've discarded Diamonds, which means that when he said Yes to the Hearts or Diamonds question, we know that he MUST have a hearts because he CAN'T have a diamonds. For iteration 2 we see he doesn't have a clubs but we also see he said yes to whether he had a clubs OR a hearts so again, we know he has a hearts! It requires a little bit more work but it's fairly obvious when we think about it. Finally we have our final possibility.

The Tester says Yes to half the combinations and No to the other half

This is when the Guesser runs into problems

Iteration	H / S	H / C	H / D	S / C	S / D	C / D
1	Yes	Yes	Yes	No	No	No
2	Yes	Yes	No	Yes	No	No
3	Yes	No	Yes	Yes	No	No
4	Yes	Yes	No	No	Yes	No
5	Yes	No	Yes	No	Yes	No
6	Yes	No	No	Yes	Yes	No

The first thing to notice is that iteration 1 and 6 are trivial, in this case there is a common suit between all the Yes's which means we can safely pick that suit (in 1's case it is Hearts, in 6's case it is Spades). The second thing to notice is 3 and 4 are also solvable because the Yes's both share the common suits and have inconsistencies. For example in 3's case there are two yes cases that contain hearts, 2 yes cases that contain Spades and 1 yes case containing a clubs and 1 yes case containing a diamonds. We can safely say that clubs are diamonds are not the suits the Tester has, so we can easily solve this problem.

The trouble occurs in iteration 2 and iteration 5, the issue is there is no way to distinguish between each iteration. In this case all we are able to do is exclude a suit, in the case of iteration 2 we can safely confirms diamonds is definitely NOT a suit and in iteration 5 we can safely confirm clubs is NOT a suit. But in this case we have three suit contenders and there's no information about which suit is the correct one.

For iteration 2 for example we know that the Tester has a hearts, spades OR a clubs, we know that out of these three the Tester has two of them that's all we can confirm. He's only given us all Yes's for any combination containing any of these 3 suits. We've effectively moved the problem into a three suit problem and this three suit problem is unsolvable, because if you guess any two of three suits you'll always get a yes, so you can just say yes all the time.

Currently I don't believe there's a way to minimize this problem which means the final answer is:

Yes the Tester can always (granted he picks up two different suits) make it impossible for the Guesser to get it right

Informal Proof Printing Money Bridges Gap Between Rich and Poor.

Informal Proof Printing Money Bridges Gap Between Rich and Poor.

One of the big questions about universal basic income (UBI) is "how are you going to pay for it?". While there are many good schemes such as increased taxes that can pay for it, there's one thing a lot of people don't consider. Why don't we just print more money?

Because of inflation right? If we printed more money than the value of money goes down and so no extra value has entered the economy, right? Yes, but I'm here to prove to you that even though no value has actually entered into the economy the poor still get richer at the expense of the rich getting poorer. How does this make sense? Lets find out.

To set up our society suppose we have an economy with some amount of total money M and some amount of total people n. We say we want to print some amount of money C to pay exclusively for universal income. We say that before applying universal basic income the total value of the kth person's worth is given by the function Q(k). Notice I used the word "value" here, value is described simply as the fraction of the total amount of money in the economy that person has, not the total amount of actual money that person has. This will become important when we start talking about inflation because after inflation money is worth less so talking about money in raw terms is not very useful, in UBI everyone gets more money. Instead we want to know how much value that person gets and so we have to make that distinction.

When we're printing new money we cause inflation, the value of a single dollar is worth less than it used to be. I am going to call the degree the value of a single dollar decreases our inflation factor and it's given trivially by this equation.

We also want to know how much money each money (not value) someone will get from UBI, if we assume the money is distributed equally the amount of money someone gets can be given as

This means the total value a person will have after UBI is given out is the total amount of money they have (the money they have initially + the UBI payment) multiplied by the new value of the dollar (the inflation factor). Describing this equation:

Factoring out we get

Great but we care about how their value changes not their absolute new value, we can calculate this by simply dividing their new value by their old value to give us.

So lets notice something here, d and j are both constants so the only variable on the RHS is the initial money we started with. The proportion of gain or loss we get is inversely proportional to the amount of money we initially had. The more money we had the more loss we should expect, the less money we have the less loss we should expect. This means that poor people should expect greater benefits from UBI than rich people even when factoring into account inflation, but how good are these benefits really?

To figure this out we should ask ourselves how much money do we need to break even, ie: not gain or lose any value after UBI. If we have more than this amount of money we should expect to lose value and if we have less than this amount of money we should expect to gain value. We can figure this out by setting the LHS side to 1 and solving.

Great! But this form of the equation is a little abstract, let us expand out the inflation factor d and the UBI income per capita j to see something quite interesting...

That's right in order to break even the amount of money you need to start with is the average amount of money in the society. If you have below average income you will GAIN value and if you have above the average you will LOSE value. Therefore printing money favours the poor at the expense of the rich! Woohoo we've solved it right?

"But surely the rich could raise prices, and then make UBI useless!"

Argh those dastardly rich! But are we actually sure that the rich raising prices will disadvantage the poor? Let us investigate, to model this we should introduce a price of a good, we'll call the value of the good G so that the number of goods (A for amount) someone can buy is simply given as

Notice that G here is once again value not money. If we were to call the value of the good after UBI is implemented (and the rich raise prices) G' then the equation:

Does NOT mean the prices of the good hasn't changed, it means the VALUE of the good hasn't changed or that the price of the good increased with inflation exactly. Noting that we will introduce a factor q which is an arbitrary factor that is how much the rich increased the items value after UBI. Giving the new value of our good as:

If q is greater than one then the rich have raised prices unfairly and if q is less than one then the rich have failed to raise prices and the poor are unfairly advantaged. If q is exactly equal to one than the rich have done the right thing and have raised the prices of the good exactly proportional to the amount of inflation. The new number of items a person can buy is now equal to their new value divided by the new value of the good.

Expanding out Q'(k) gives us our final equation

We want to know whether someone can buy MORE goods or LESS goods so we divide the new amount of items someone can buy with the previous amount of items someone can buy

Doing some cancelling we get

Cool! So now we know how much more a specific person can buy but once again we want to know who is advantaged (can buy more) and who is disadvantaged (can buy less). To figure this out we once again set our LHS to 1 to find out what value you need to break even, if you are above that value you will be able to buy less and if you are below that value you will be able to buy more. Solving we get:

Great! Somethings to note here. Lets suppose prices do not change with inflation, what happens here? In this case q is exactly equal to the inflation factor d which means we get a division by 0, that seems broken but it's not it just means there is no solution to this equation which means no matter how much money you have you'll ALWAYS be able to buy more goods. This makes sense because again, everyone gets more money so if the prices don't change to reflect that then everyone's buying power increases.

Ok but what happens if the rich do the right thing and increase their prices with inflation, in this case q just becomes 1 and we get this familiar equation again:

Low and behold that's the exact same equation we got before and once again when we expand d and j we get.

That's right even if prices increase with the resulting inflation the poor still can buy more if they have less than the average income. Why? Because even if the rich get the same value for the goods that they're selling the value still initially changed to favour the poor when UBI was introduced so the poor STILL have more buying power even when you take into account a price increase.

What if the rich raised the prices even more, beyond inflation? First of all, yes this certainly COULD happen but the rich don't need UBI to do this, they can increase prices unfairly right now! The mechanisms that are stopping the rich from raising the prices of goods arbitrarily high right now will still exist even after UBI is implemented. But suppose the rich did raise prices higher than inflation, what would happen? 

Well you can plug in some random values of q, any value greater than 1 unfairly favours the rich and any value less than 1 unfairly favours the poor. But for values greater than 1 you'll notice something, there will always be an amount of money that you can have, below which, you will be able to buy more items. When q is greater than 1 the rich do get richer and the middle class gets poorer but the lowest class STILL manages to get richer, this stops becoming true when q is so high that the amount of money you need to have less of is smaller than the price of a single good. Can the rich raise prices so drastically high? Of course, but again whether they could do that isn't a question of UBI, they could raise prices this high with or without UBI and it'd have the same effect, people can buy less items.

Anyway I hope that clears up why printing money to pay for UBI can still have a beneficial effect on society.